Microbiology Serial Dilution Calculations

Serial Dilution

DILUTIONS: Principles and Applications David B. Fankhauser, Ph.D., Professor of Biology and Chemistry.

How to Work Microbiology Dilution Problems. Dilutions are useful in science when making solutions or growing an acceptable number of bacterial colonies to count.

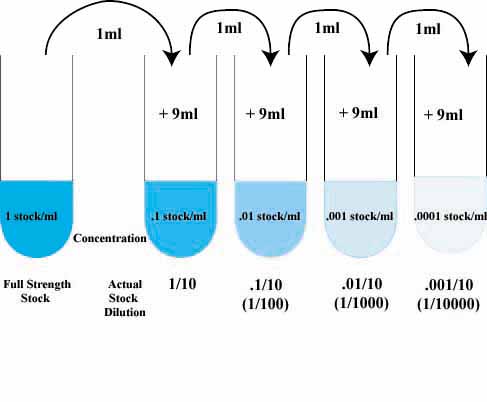
Now that you are very comfortable with dilution factors what happens if you dilute and then dilute again. For example, we could take super-strong cofee, dilute it by 1/5, then dilute THAT by 1/10. So,

To find the overall or total dilution factor,

simply multiply the dilution factors for each step.

Once again, here s an applet to practice finding the total dilution scheme, regardless of how the dilution scheme is expressed -- as directions, as fractions, or as decimals.

Remember, keep going until you re very comfortable with the calculations Oh, and do yourself a favor, use a calculator..

Given the following series of dilutions,

what is the total dilution factor.

So let s put some of these skills together to design dilution schemes -- you don t want to be a lab grunt all your life, right.

So to do this, you need to figure out the overall dilution you re shooting for. In this case, just take the concentration you want to achieve, and divide it by the concentration you currently have. As an example, if you want coffee with 5 caffeine molecules per mL, but the coffee you have has 5000, you need a dilution of 5/5000, or 0.001.

The trickier part is figuring out a series of dilutions that will achieve your overall dilution. In these examples, the numbers will always come out evenly if you choose dilutions of 1/2, 1/5, 1/10, or their multiples. Use the scratchpad to check your plans, and if you get completely lost, click the. button for a workable dilution scheme.

You might not be able to do this in your sleep, but at least work at it until it makes sense

You have a stock with an estimated 40,000 CFUs per mL, and you need to dilute to an estimated 500 CFUs per mL.

What overall dilution factor do you need.

How could you achieve this total dilution in three steps.

test your dilution factors here :

So far we ve figured out how to make a dilution, which we can then plate and count. But by definition, we re counting only a fraction of what was originally there. How do we account for that. By scaling up.

Scaling up means starting from a sample and figuring out how many were in the original brew, or stock, or whatever was originally there.

For example, we can start with a cup of wimpy coffee and figure out how much caffeine was in the original brew. All we need to know is what the overall dilution factor was. In the case of wimpy coffee, it was 1/50, or 0.02.

So, when we count the caffeine molecules in a cup of wimpy coffee, we know we got 1/50th of what was in a cup of the original brew -- or in other words, there was 50 times as much in a cup of the original. This method is called multiplying by the inverse of the dilution factor.

If the dilution factor is in the form of a fraction,

i.e., 1/50 becomes multiply by 50/1.

If the dilution factor is in decimal form,

multiply by 1 over the decimal

i.e., 0.02 becomes multiply by 1/0.02.

Finally, notice that I m telling you the total number of caffeine molecules ONE CUP of the original brew. If I don t know the actual amount of original brew, I also won t know how much caffeine there was total.

Here are some problems, ranging from easy to a bit hard

I did a series of dilutions with an overall dilution factor of 1/20,000, and then plated a grew a 1mL sample. After 1 day, I counted 27 CFUs on the petri dish. How many CFUs would there be per 1mL of the original stock.

To make this problem interactive, turn on javascript.

I think I have the answer:540,000 per mL

I did a series of dilutions, with dilution factors of 0.1, 0.1, and 0.01. At the end I plated and grew a 1mL sample, and counted 48 CFUs. How many CFUs would there be per 1mL of the original stock.

What s the overall dilution factor.

overall dilution factor 0.1 0.1 0.01 0.0001

I think I have the answer: 48 1/0.0001 480,000 CFUs per mL

I did a series of dilutions as follows:

If the final 1mL sample had 152 colonies, what was the original concentration.

The dilution factors were 1/10, 1/100, and 1/50

The overall dilution was 1/50,000

I think I have the answer:152 50,000 7,600,000 cells/mL

Once again, let s take a breather from the theory and practice. This is one of the do-it-in-your-sleep kind, and it has two steps:

Look at the dilution scheme to determine the total dilution factor

Look at the plate and scale up to determine the total CFUs per mL.

Your browser does not support html canvas. There were CFUs on the plate.

Remember the picture of the hell-to-count petri dish with 500 colonies. No one wants that to happen to them, especially late on a Friday afternoon. But on the other hand, how can we avoid it.

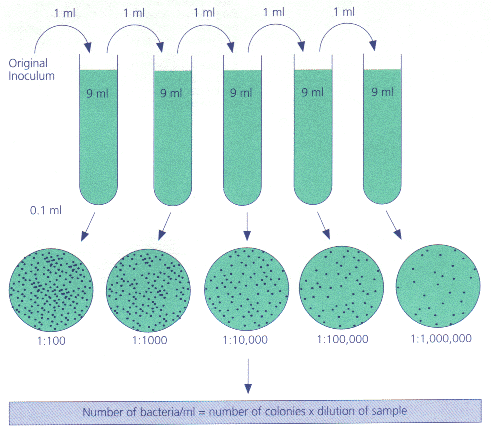
Very easily while we re doing our dilutions, we just keep plating each intermediate step. Then the next day, we decide which plate looks like the most reasonable for counting. Since we cleverly labeled each plate with its overall dilution factor, we also know how to scale back up to get the original concentration.

So, now we finally have all the pieces of serial dilution assembled:

To make things easier, the standard operating procedure is to go by factors of 10, and to do about 5 or 6 plates altogether.

Content on this page requires a newer version of Adobe Flash Player.

Let s say I guesstimate that I have about 42 million CFUs per mL -- I might want to start with a first dilution of about 1/1000, and plate that. Then I make 4 more 1/10 dilutions, plating each one in turn. In the end, I have 5 plates, labeled as shown below. And, if you roll over the image, you will see the plate counts I expect if my original guess 42 million was approximately correct. Oh, and TMTC means Too Many To Count.

For this, we have any easy rule of thumb: the plate you count should have between 30 and 300 colonies. Use your mouse below to see how this works.

This rule of thumb has the undeniable advantage of being easy to use. But why does it work.

Let s imagine that we have a sample with exactly 42 million cells per mL. And let s say that our technique is flawless. If we count a 1:1,000,000 diluted plate, we should find exactly 42 CFUs remember, we have magically flawless technique. But the exact same thing would happen if our sample started with 42,000,001 cells. Or 42,001,000 cells. Or even 42,100,000 cells. In fact, even with our absolutely flawless technique, the best we can say is that there are between 41,500,000 and 42,500,000 cells. So our absolutely unavoidable error is plus or minus 500K/42million -- about 1.1. That s pretty good.

Let s look at some other ways we could count the same 42 million cell sample:

NOPE, can t do it, this is too much to count

SORRY, still too hard to count

chimpanzees can count this plate.

The more we dilute, the easier the counting, but the higher the error. So you can see that the 30 to 300 guideline is really a compromise between countability and error.

Here is a chance for you to put all of the steps together, using viable plate count and serial dilution to quantify a bacterial population

Here is some practice with different dilution schemes. This time the applet will do the counting for you. The first problem should be very easy at this point, but after that you can click on Hard Problem to get trickier dilution schemes.

Below are a few unusual situations things do go wrong, of course, and you should be able to recognize that. If you think the dilution series is not valid, click on re-do the dilution.

Remember Frank. He s still sitting on the examining table with a coat over his head. In fact about 50 of people with meningitis will die when the bacterial levels in their blood stream reach 500 / mL.

The worried nurse hands you a vial of 10 mLs of Frank s blood. How can you decide whether the infection is at a lethal level.

What counting method will you use.

Unfortunately, a direct count or a photospec would require separating the meningicocci from the red blood cells. If we could do that, we could probably just cure poor Frank. So we re stuck with a viable plate count.

What dilution scheme will you use.

We need to get plate counts between 30 and 300, and we think that the concentration in his blood might be as high as 500 per mL, but it could be much lower. So, we should go ahead do the first plate without even diluting. After that we could do standard 1/10th dilutions.

How many dilutions do you need.

You definitely need at least 1 dilution, in case Frank is somewhere in the 300 or 400 per mL range. Without a dilution, that wouldn t be countable.

But really, a single 1/10th dilution would suffice. If Frank has 300 colonies in a 1/10th dilution, he has 3000 actual cells per mL, and that would be fatal. Of course, he d also be dead, but let s not be morbid.

However, you could keep going with a standard 5 dilutions and not waste much time or energy, plus it would allow you to make an accurate estimate regardless of his actual level of meningicocci in the blood.

Make sure you understand the following concepts -- go back to the applets if you need to:

dilution factor stated as a fraction or decimal

overall dilution factor product of individual dilution factors

choosing the plate to count 30 to 300 CFUs

scaling up from the plate to the population size multiplying by the inverse

setting up an appropriate dilution scheme to result in a countable plate

If you want a printer-friendly version of this module, you can find it here in a Microsoft Word document. This printer-friendly version should be used only to review, as it does not contain any of the interactive material, and only a skeletal version of problems solved in the module.

Let s say a culture contains about a million CFUs. At 1 CFU per second, that would take 11.6 days to count. Assuming you didn t stop to eat or sleep.

Clearly a better way is needed.

And clearly, this module is going to pick that method apart and pound it into the figurative whiteboard.

First of all, we re going to use the Viable Plate Count method -- the only method that can tell a live cell from a dead one for a rundown on counting methods, look here. So, we re going to take a little bit of our culture, put it on a plate, and grow it up. But we still have a problem -- too many colonies to count. For example, even 500 colonies on a petri dish would look something like this:

What if you are trying to count a population in the thousands or millions. You could literally have a carpet of colonies also known as a confluent lawn growing on your petri dish. This is where dilution saves the day. Not just dilution, but serial dilution meaning dilution over and over again.

Why do we dilute. To have less to count

Why do we do it repeatedly. Because we don t know how much dilution we need. Every time we dilute, we ll also make a new plate to incubate. So we might do 5 dilutions and grow up 5 plates. Then we ll end up throwing away 4 of them. Sound wasteful. Well, dilution and plating is quick and easy compared to the pain of starting your experiment all over again.

Of course, lots of things can be diluted, not just blood samples

So let s see what the process of diluting looks like.

Cold Press coffee is a superstrong form coffee that starts out with about a zillion molecules of caffeine per cup. In order to actually be able to drink the stuff, you have to dilute it.

For example, you could put one cup of cold press coffee into a pot and add 9 cups of water.

How many molecules of caffeine are in the pot.

How many cups of coffee are in the pot.

If you pour 1 cup from the pot, how many molecules of caffeine will it have.

Let s look at this in graphical form:

Simple, right. Of course, we don t want to have to draw pictures every time we do a dilution, so we could simply write:

1 cup coffee 9 cups water -- 1/10th as strong as the original.

The MicrobeLibrary includes peer-reviewed visual resources and laboratory protocols for undergraduate microbiology serial dilutions calculate this dilution.

• Video embedded  Working with billions of tiny cells can pose a problem when you need to count the total number of cells in a sample. Fortunately, through precise serial dilution of a.
• Overall dilution. Now that you are very comfortable with dilution factors what happens if you dilute and then dilute again. For example, we could take super.
• WORKING DILUTION PROBLEMS It is a common practice to determine microbial counts for both liquid and solid specimens---suspensions of E. coli in nutrient broth.
• SAMPLE MATH PROBLEMS FOR MICROBIOLOGY Calculate the CFU/100 mL in the original culture. 4. A serial dilution was prepared by adding 0.1 mL to 9.9 mL.
• A dilution is a reduction in the concentration of a solution. A serial dilution is a series of repeated dilutions that provides a geometric dilution of the original.